- On ne pourra pas y mêler CPU et systèmes d'Entrées/ Sorties, car les demandes sur ces deux centres ne peuvent pas être identiques.
- Il est difficile dans la pratique d'équilibrer parfaitement un système d'Entrées/ Sorties.
Ce type de modèle offre en revanche un certain nombre d'avantages :
- C'est une bonne approximation pour un système borné par les E/S.
- Il plus précis que les déductions effectuées par bornes asymptotiques.
Le calcul ici proposé permet d'encadrer le débit du système et le temps de réponse en délimitant les demandes sur chaque service que demanderont les transactions. Connaissant le nombre d'Entrées/ Sorties nécessaires à l'exécution d'un batch, on peut calculer D. D
(le nombre d'Entrées/ Sorties sur chaque disque) variera en fonction du nombre de centres K entre les bornes 
et 
. Nous utiliserons l'exemple suivant afin d'illustrer les résultats obtenus :
On considère que chaque transaction nécessite 18 Entrées/ Sorties de 12ms (quelque soit le disque) chacune. En en déduit D=18*0,012=0,216. En fonction du nombre de disques, et sachant que le système est équilibre, on abouti aux résultats suivants:
Nombre de disques |
Nombre d'E/S/disque |
D |
4 |
4,5 |
0,048 |
3 |
6 |
0,072 |
2 |
9 |
0,096 |
2.1 Cas des traitements batchs
Le calcul de base s'appuie sur la fonction qui donne l'utilisation d'un centre en fonction de la population N présente dans le système :
 |
(la démonstration de ce théorème est donnée en paragraphe 2.3)
On peut d'après la loi de Little exprimer le débit X(N) du système en fonction de la population et de la demande de service à chaque centre par :
 |
D'où :
 |
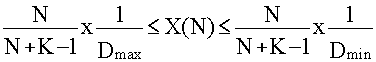et le temps de réponse R(N) est encadré par
 |
On peut trouver une seconde borne optimiste obtenue par la constation intuitive suivante:en supposant que le système ne soit pas équilibré, et que la charge de travail demandée au système soit forte, l'utilisation de chaque centre augmente, sans pour autant dépasser 1. Le centre le plus sollicité, celui pour lequel la demande est , est tel que :
et
2.2 Cas des traitements interactifs
Les formules deviennent
 |
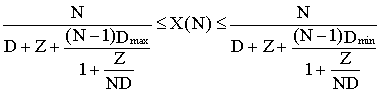et
 |
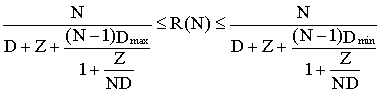La démonstration est similaire à celle donnée pour les traitements batchs, en tenant compte du fait que l'évolution du temps de réponse en fonction du débit est
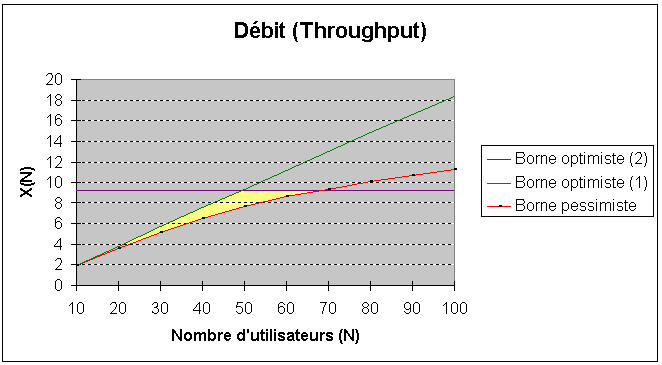
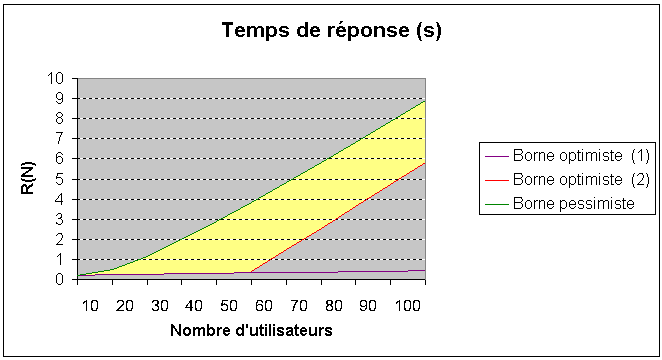
On obtient les courbes de débit et de temps de réponse (on utilise pour cet exemple un temps de réflexion pour Z=5s).
